───✱*.。:。✱*.:。✧*.。✰*.:。✧*.。:。*.。✱ ───
A function is a special relationship from to , where and are both sets, where elements of relate to exactly one element of .
Each element in the domain (set ) maps to at least one element in the codomain (set ). No element in the domain can be mapped to more than one element in the codomain.
Terms
- Domain → the values that can be in
- Codomain → the set of values that can be in
- Range → all values of that produces for a given
Examples
- Valid Function →
- Invalid Function →
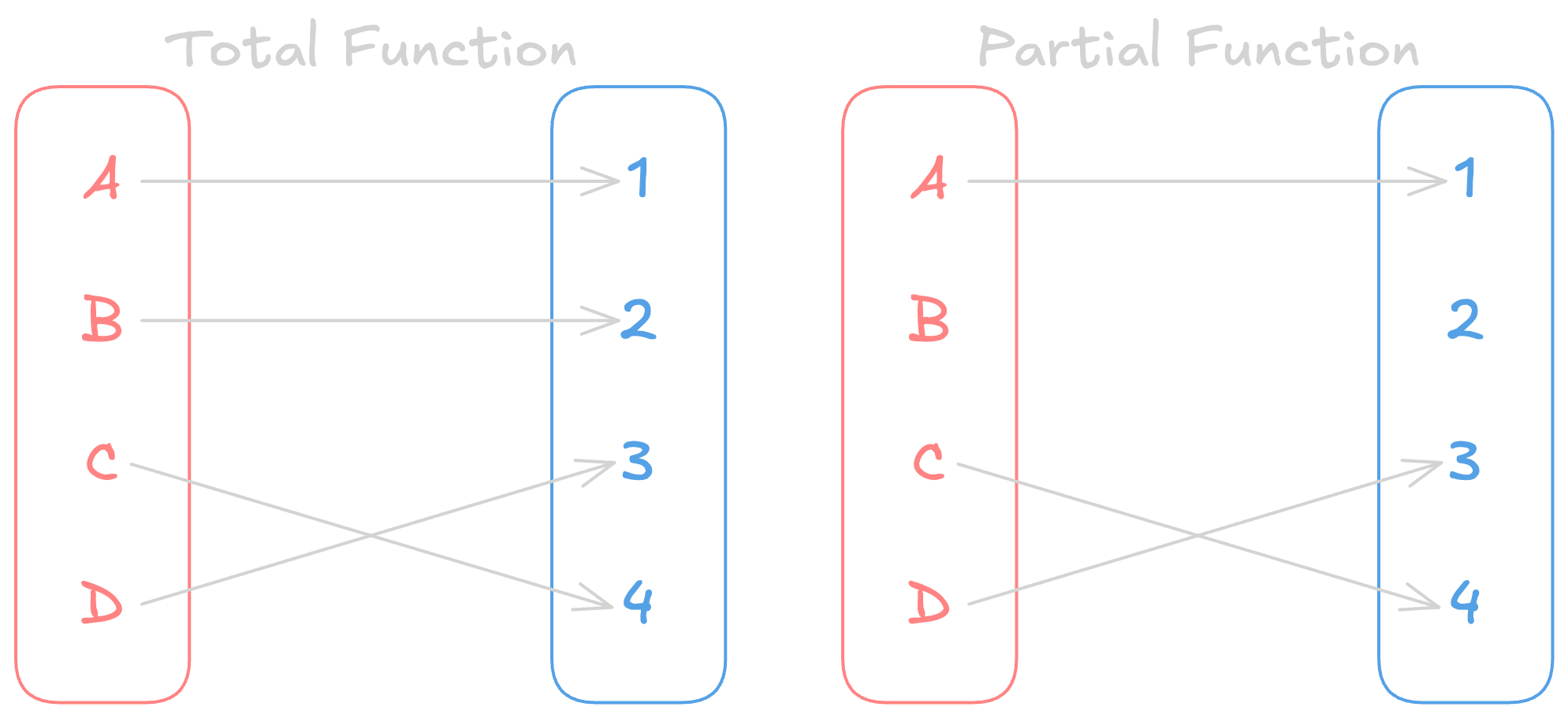
Total Functions
- Also known as “defined everywhere functions”
- Every element in the domain is mapped to an element in the codomain, such as
- Total Function →
- Partial Function → → only defined for , not
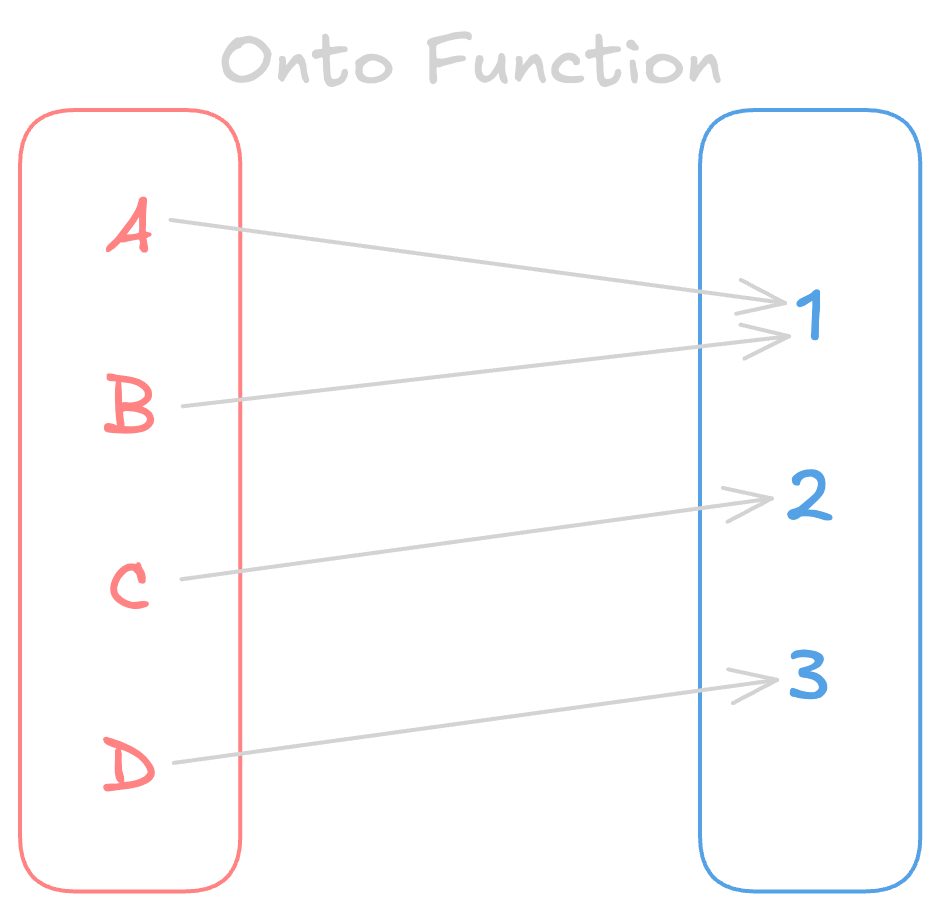
Onto Function
- Every element in the codomain is mapped to at least one element in the domain
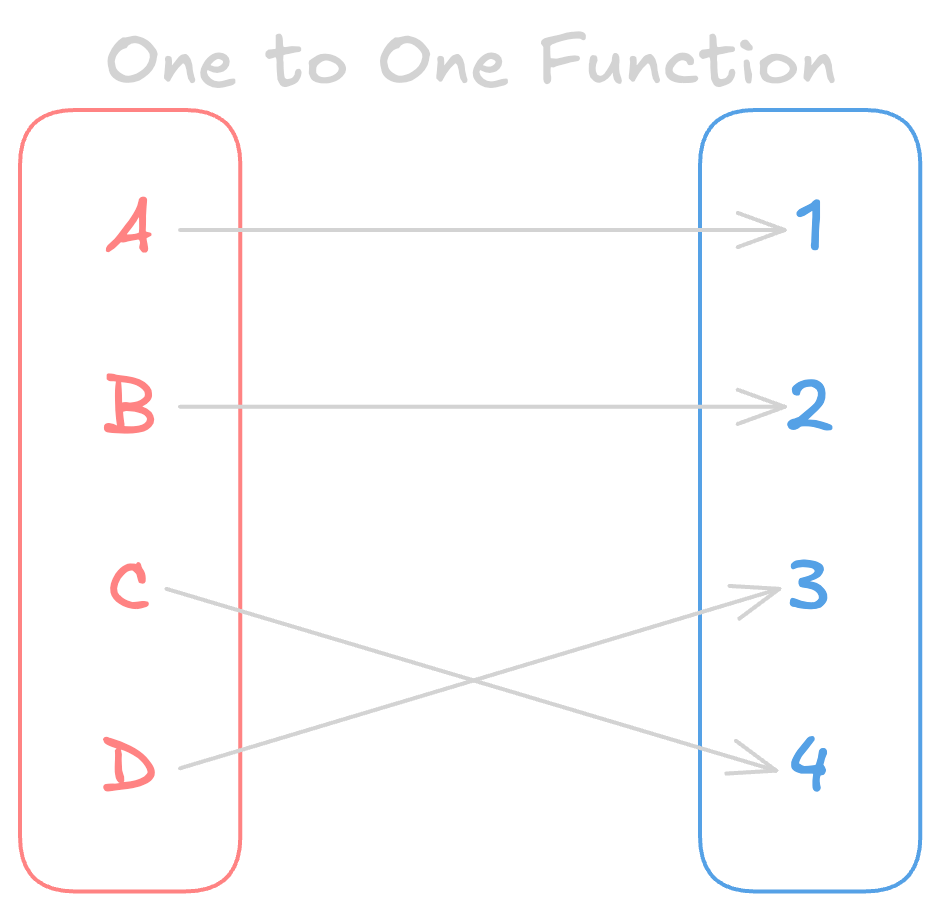
One to One Function
- Every element in the codomain is mapped to at most one element in the domain
Inverse of a Function
- A function is invertible if and only if is both one-to-one and onto.
- Given , one can deduce
-
One Way Function
- Given , one cannot deduce
Hashing Functions
- Encryption can be decrypted (two-way function)
- Hashed passwords cannot be decrypted (one-way function)
Function Composition
- Functions can be combined/nested with the syntax or
───✱*.。:。✱*.:。✧*.。✰*.:。✧*.。:。*.。✱ ───