Relations

───✱*.｡:｡✱*.:｡✧*.｡✰*.:｡✧*.｡:｡*.｡✱ ───

A relation is a subset of the cartesian product of two or more sets based on a rule or definition. It is typically denoted with , , , or .

A relationship between two sets and is a subset of , meaning it contains some ordered pairs from the cartesian product.

Examples

• Given and
  • A relation, , on is defined as to whether a human owns the Animal.
• Relations can also be across a single set
  • Given ,

Domain

• The domain of a relation is written as .
• If is a relation on , then is the subset of all in where and .

Range

• The range of a relation is written as .
• If is a relation on , then is the subset of all in where and .

Matrix Representation

• Place a 1 where the relation is included in the cartesian product, otherwise place a 0.
• Given and and the relation

Directed Graph Representation

• A way to represent a relation visually
• Left nodes represent elements of and right nodes represent elements
• A directed edge (→) from to if and only if

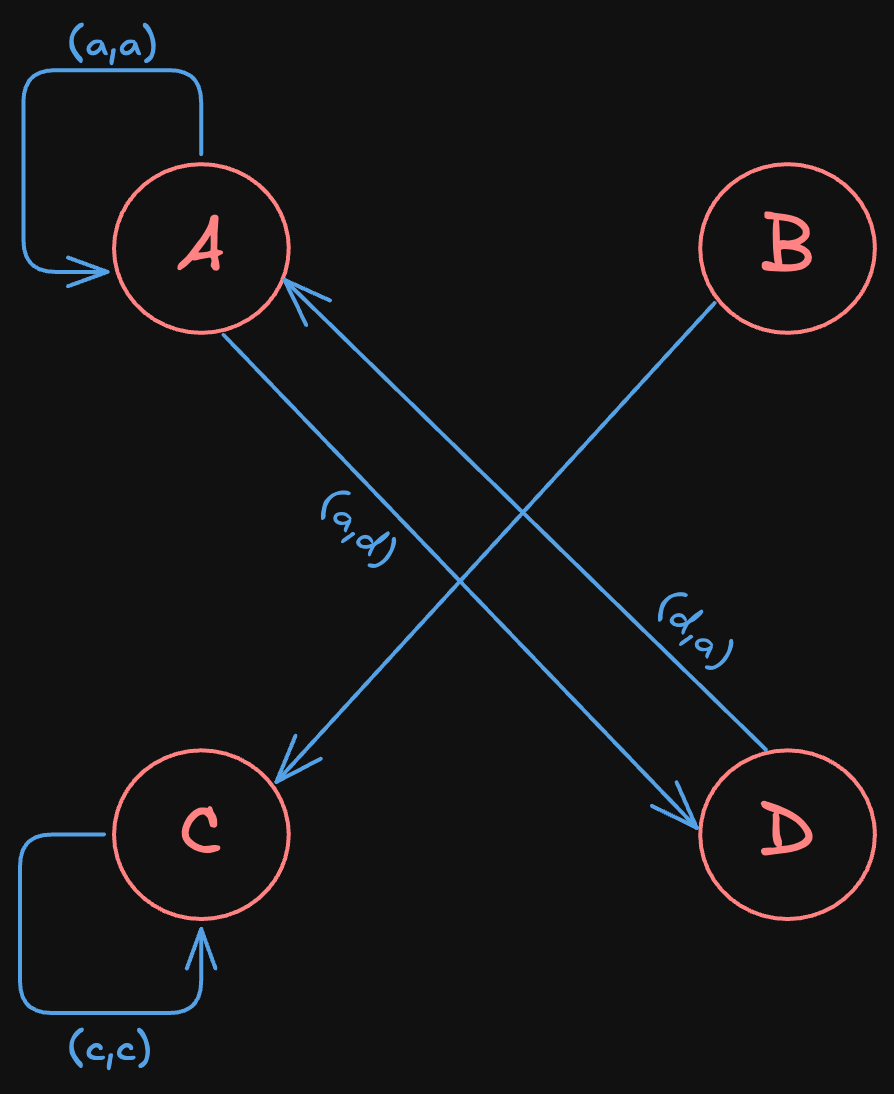
In-Degree

• The number of times an element is the second element in an ordered pair
• Visually, the number of arrows pointing inwards

Out-Degree

• The number of times an element is the first element in an ordered pair
• Visually, the number of arrows pointing outwards

Properties of Relations

Reflexive

Symmetric

Transitive

Equivalence

• A relationship is equivalent if the reflective, symmetric, and transitive properties are all true.

───✱*.｡:｡✱*.:｡✧*.｡✰*.:｡✧*.｡:｡*.｡✱ ───