Correlation

───✱*.｡:｡✱*.:｡✧*.｡✰*.:｡✧*.｡:｡*.｡✱ ───

Correlation measures the relationship between two variables, including the strength and direction between them.

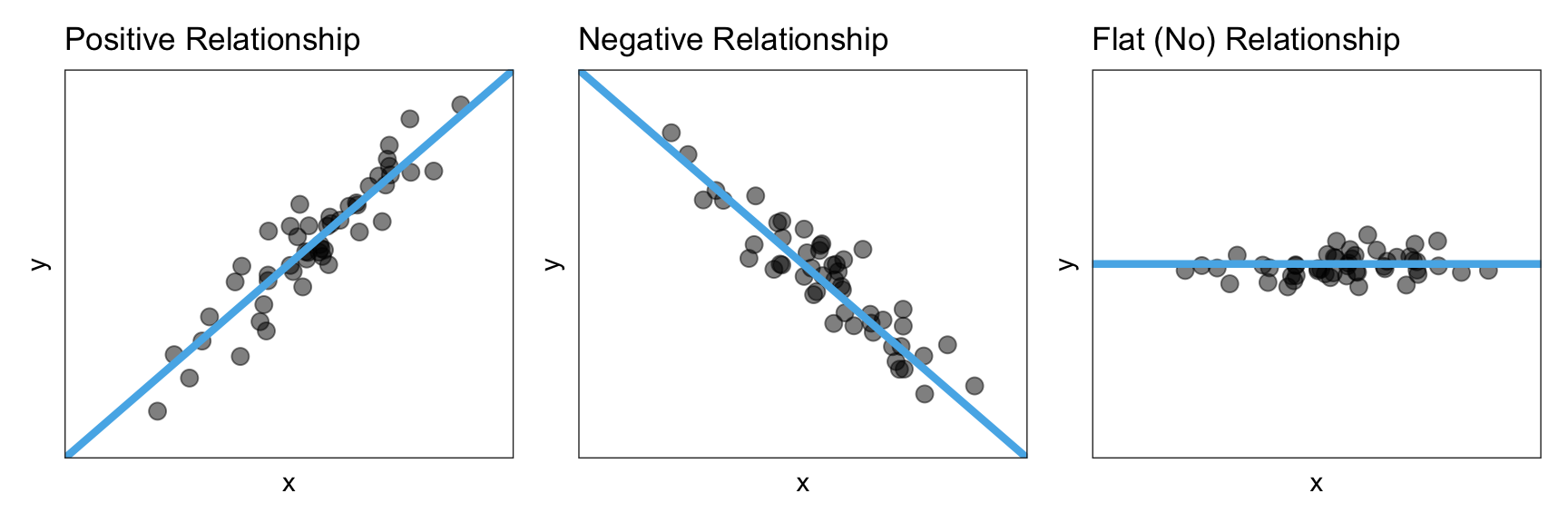
Directions

• Either positive, negative, or flat (no relationship)

Mean

• → mean
• → individual value

Standard Deviation

• Measures the average deviation of the data from the mean

Variance

• Measures how spread out the data is form the mean
• Units are squared units of the data. If is in , variance is

Covariance

• measures how 2 variables vary together
• Positive → both increase/decrease together
• Negative → one increases and the other decreases
• • Similar to the variance formula, but we use rather than squaring

Correlation Coefficient

• Referred to as , where

Strength

• The magnitude of represents the strength of the relationship
  • → perfect
  • → strong
  • → medium
  • → weak
  • → no relationship

Direction

• Positive → variables increase together
• Negative → variables move in opposite directions

───✱*.｡:｡✱*.:｡✧*.｡✰*.:｡✧*.｡:｡*.｡✱ ───